
When it comes to carbon dioxide emissions, how inefficient are separate markets versus a single market? Inefficiencies in separate markets are mitigated when firms that own plants across multiple markets participate in a single integrated market.
Economists have long advocated for market-based solutions to correct environmental externality problems such as harmful emissions from combustion of fossil fuels, in place of traditional command and control regulations.
A well-known example of a market-based solution is to create a market for emission permits. In this market, polluting firms have to carry enough permits for every ton of emissions they pollute. Firms that tend to emit more need to buy permits, while firms that reduce emissions through their own efforts can sell their excess permits for a profit. In theory, market-based solutions leave the guesswork out of regulators’ hands, and let firms decide the best way to reduce emissions.
For market-based solutions to be effective, one has to cover multiple jurisdictions to take advantage of trade gains from heterogeneous polluting sources. Efficiency requires that the marginal abatement cost across sources be equal, otherwise it would be beneficial to shift abatement from higher cost sources to lower cost ones. With the United States planning to withdraw from the Paris Climate Accord, the future of a coordinated, global solution to climate change seems bleak. Only separate markets, at best, may be feasible due to the difficulty of coordinating regulations across jurisdictions, be it states within a given country such as the U.S., or individual nation-states.
The near-infeasibility of organizing a single market raises the question to what extent having separate markets will be an adequate substitute for a single market. We seek to answer this question in a recent project that we summarize in this article.1 The project’s main objective is to empirically address this question by examining the relative economic efficiency of single versus separate markets in an actual, real-life setting.
The near-infeasibility of organizing a single market raises the question to what extent having separate markets is an adequate substitute.
Motivation
Our work is motivated by recent failures to coordinate environmental policies across states or countries. One such example that closely motivates our work is the current legal and political challenge to the U.S. Clean Power Plan (CPP), a federal regulation based on the Clean Air Act that sets CO2 emissions limits from electric power plants for 2022 to 2030. Although the CPP is designed as a federal mandate, the final form of CO2 regulation is likely to be at the state level.
There are two reasons that CPP implementation may be at the state level. First, the Clean Air Act only authorizes the U.S. Environmental Protection Agency (EPA) to set targets at the state level and solicit state implementation plans to achieve these targets. Second, the Trump administration ordered a CPP review in March 2017 that may delay or even terminate efforts to regulate CO2 emissions at a federal level. If the second and less optimistic scenario materializes, any regulation of CO2 emissions will be a state-level effort.
A second example is the withdrawal of the United Kingdom from the European Union (EU). This process, known as Brexit, may imply a UK departure from the European Union Emissions Trading System (EU-ETS) as well, and force the UK to create its own carbon market. The discussion of which type of environmental policy the UK can implement by itself has already started. This is particularly important in light of the fact that, while the UK pledged a 57% emission reduction in the Paris Agreement, the EU as a whole was less ambitious, proposing only a 40% reduction (Hepburn and Teytelboym, 2017).
Setting
We estimate a structural model of production and investment decisions, and use this model to simulate firms’ behavior under single and separate CO2 markets. We use data from electric utilities that participate in the Pennsylvania-New Jersey-Maryland (PJM) wholesale electricity market and consider CO2 emissions regulation implemented through the Clean Air Act. PJM operates one of the world’s largest wholesale markets as the regional transmission organization that covers 13 states.
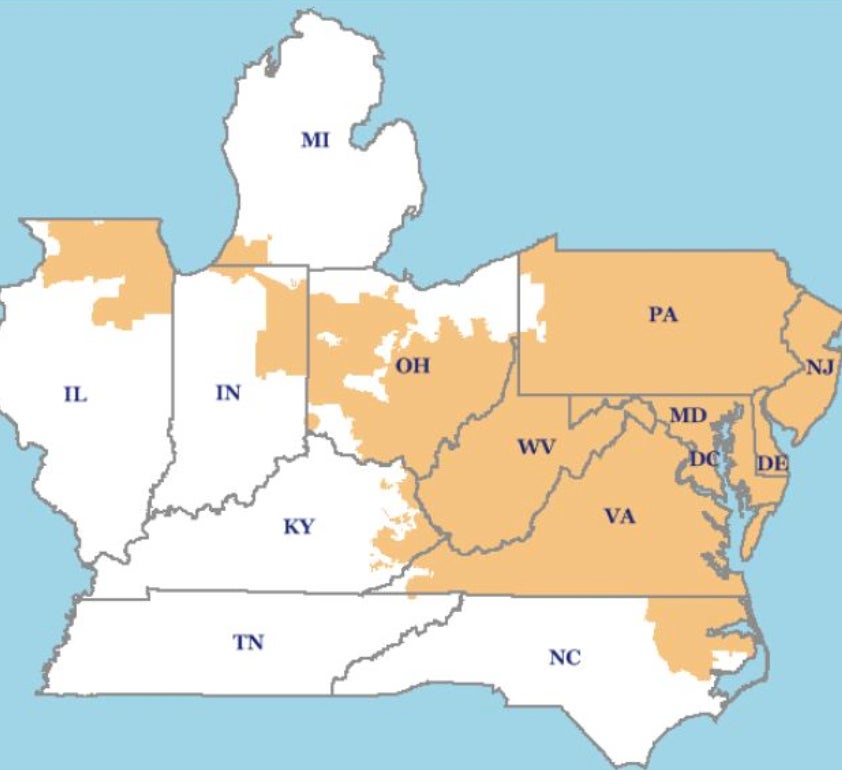
Figure 1 shows the PJM footprint. Electric utilities own plants scattered across these states. Plants generate electricity that is then sold in the PJM wholesale market and distributed across the region. In terms of CO2 emissions regulation, the Clean Air Act authorizes the EPA to set state-wide emissions limits for existing plants, and separate source-specific regulations for new plants. Although states are free to coordinate and meet the targets as a group, the EPA does not have the authority or power to compel states to do so, even if it would be efficient from a social welfare objective.
The main economic insight of our policy digest is that the negative effects of separate markets for CO2 emissions are greatly mitigated by firms’ participation in an integrated wholesale market for electricity. Facing an integrated electricity market, firms will optimally make their output and investment decisions, taking into account the allocation of production and the resulting distribution of CO2 prices across markets. All else equal, profit-maximizing firms move production from markets with higher CO2 prices to markets with lower CO2 prices. In a frictionless environment, output reallocation and CO2 price readjustment will lead to convergence of CO2 prices, as if there were a single market for emissions. In practice, frictions exist that would prevent perfect reallocation of output and readjustment of CO2 prices. Here, we focus on capacity constraints as the main friction and this is the motivation for including investment in new generating capacity in our analysis.
In a frictionless environment, output reallocation and CO2 price readjustment will lead to convergence of CO2 prices, as if there were a single market for emissions.
Model
Our model consists of a set of firms that own portfolios of plants across different states. Differences in plant age, technology, and location affect the cost of electricity generation. In each period, firms produce electricity using their existing plants and sell it in the PJM wholesale electricity market. Although the wholesale electricity market is approximately competitive due to forward contracts (Bushnell, Mansur, and Saravia, 2008), we assume that investment decisions are strategic in the sense that firms take into account capacity reactions by rivals and the impact of investment on future prices, similar to the model in Dixon (1985). Firms decide how much to invest in coal- and gas-fired generation. Investment in new capacity allows firms to produce at lower cost and, potentially, increase profits from electricity sales in subsequent periods.
To capture in a realistic way firms’ supply decisions and incentives to invest in response to regulation, we need a model that preserves the heterogeneity of costs across plants, and tracks their evolution as firms add new capacity. Plant costs depend on a number of factors: efficiency (heat rate), emission rates for various pollutants and associated compliance costs, fuel prices, and other operations-and-maintenance (O&M) costs. As a result, a high-dimensional state vector is required to track the evolution of all these factors for the existing plants and the new capacity in which firms invest.
Our approach is novel and consists of leveraging on the observation that new capacity will be infra-marginal in the wholesale electricity market–—at least, in the medium run. Because of this, it suffices to keep track of the average heat and emission rates of cumulative investment over time. As a result, we substantially reduce the dimension of the state vector, which significantly alleviates the computational burden for our structural model while still incorporating the relevant information on plants’ costs.
We construct estimates for plant-level marginal cost using information directly from the data (Bushnell, Mansur, and Saravia, 2008; Mansur, 2007); Firm-level marginal costs are then step-functions, where each step represents a firm’s plant. To get investment costs, we estimate the model using the two-step approach in Bajari, Benkard, and Levin (2007), following closely the application in Ryan (2012) and Fowlie, Reguant, and Ryan (2016). The production and investment cost estimates (together with demand and fuel cost estimates) allow us to predict supply and investment decisions of firms facing CO2 emissions regulation, and we solve a series of dynamic investment problems for single and separate markets to compare outcomes across these two counterfactual scenarios.
Results
Table 1 contains our main results. Dollar values are present discounted lifetime values from 2013 onward. New capacity is cumulative investment from 2013 until 2030.
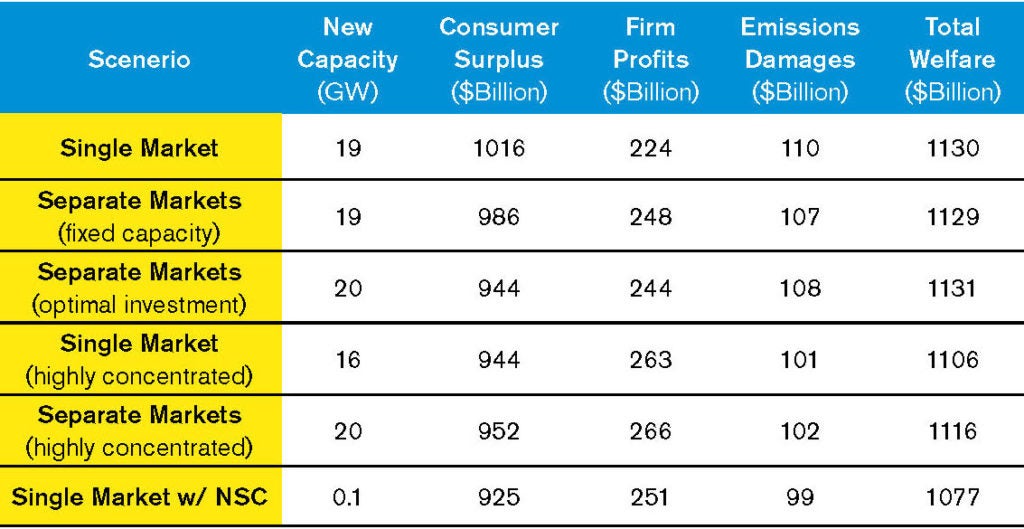
Fixing capacity and investment to be equal for both single and separate market scenarios, we find welfare losses of at most $1 billion under separate markets. Note that this loss is relatively small: It reflects less than 0.1% of welfare. In other words, the ability of firms to reallocate output alone allows separate markets to achieve almost the same welfare outcome as with a single market.
If we allow firms to optimally invest in response to the type of CO2 market(s) they face, we actually find welfare across the two scenarios to be closer to equal or even higher under separate markets in cases where investment is concentrated to a few firms.2 The reason is that investment incentives are stronger in separate markets.
Intuitively, since firms under separate markets do not have the option to buy permits from potentially lower cost units in other markets, CO2 compliance costs are higher, leading to greater increases in plants’ generating cost. But greater increases in cost can encourage more investment as long as new capacity has a sufficient cost advantage relative to the “ex-post” marginal plant. Of course, this will depend on several factors such as: the existing plant portfolio, characteristics of marginal and infra-marginal plants for each possible investment choice, evolution of new capacity efficiency, and investment cost—which stresses the importance of having a model that preserves the rich heterogeneity of plants within and across firms.
An important point in our exercise is that CO2 regulation under the Clean Air Act treats existing and new capacity differently. Essentially, existing capacity pays a CO2 price while new capacity does not. However, new capacity is required to meet a specific emissions standard, so it does not necessarily mean new capacity is fully exempt from regulation. This institutional feature influences our results, since new capacity becomes very attractive relative to existing capacity. Nevertheless, new capacity tends to be more efficient and cleaner than existing capacity. In fact, although there will certainly be emissions “leakage,” i.e. output intended to be produced by existing plants now going to essentially unregulated new capacity, emissions damages are actually lower with separate markets.3
To combat emissions leakage to new capacity, policy-makers allow states to adopt what is called a “New Source Complement (NSC).” If a state decides to adopt the NSC, the allowed emissions of the state will be increased by some amount that depends on forecasted future load. The idea is that future load will be met by investment, and the emissions limit will be adjusted accordingly via the NSC. Note however that the NSC is built-in ex-ante, that is, before investment actually materializes, and cannot be conditioned on investment. Otherwise, existing and new capacity will have different CO2 prices. This means that firms will optimally decide on the level of investment after the limit has already been increased with the NSC, i.e. a more lax regulation. As we see in the table, this drastically decreases investment and leads to welfare inferior outcomes. The takeaway here is that any form of adjustment based on future action has to be carefully thought of so as not to introduce perverse and unintended incentives.
Mike Abito
Assistant Professor of Economics, Ohio State UniversityJose Miguel “Mike” Abito is an Assistant Professor of Economics at Ohio State University. He is a reviewer for the Kleinman Center and was previously an assistant professor of business economics and public policy at the Wharton School.
Bajari, P., C. Benkard, and J. Levin (2007): “Estimating Dynamic Models of Imperfect Competition,” Econometrica, 75, 1331-1370.
Bushnell, J., E. Mansur, and C. Saravia (2008): “Vertical Arrangements, Market Structure, and Competition: An Analysis of Restructured US Electricity Markets,” American Economic Review, 98, 237-266.
Dixon, H. (1985): “Strategic investment in a competitive industry,” Journal of Industrial Economics, 33, 483-500.
Fowlie, M., M. Reguant, and S. Ryan (2016): “Market-based emissions regulation and industry dynamics,” Journal of Political Economy, 124, 249-302.
Hepburn, C. and A. Teytelboym (2017): “Climate change after Brexit,” Oxford Review of Economic Policy, 33:1, S144-S154.
Mansur, E. T. (2007): “Upstream Competition and Vertical Integration in Electricity Markets,” Journal of Law and Economics, 50, pp. 125-156.
Ryan, S. (2012): “The Costs of Environmental Regulation in a Concentrated Industry,” Econometrica, 80, 1019-1061.
- This article is based on the paper “Separate Markets for Externalities: Regional versus State-by-State Regulation of a Global Pollutant” by Mike Abito (Wharton), Chris Knittel (MIT), Kostas Metaxoglou (Carleton), and Andre Trindade (FGV). [↩]
- For example, in the case where the top 10 utilities coordinate investment decisions, BAT capacity under separate markets is 20 GW compared to 16 GW under a single market, which leads to $10 billion higher welfare under separate markets. This gap narrows down quickly however as more utilities decide their investment independently. In the case of free entry and zero profits, we find that investment and welfare under the two scenarios are exactly equal. [↩]
- It is slightly higher when investment decisions are highly concentrated, however the difference is not huge. [↩]

